Finding package dependents in Arch Linux using Pactree.

While trying various desktop environments, I noticed an unusual process called tracker3-miners consuming high CPU usage. It was not burst consumption, it was consistently hitting 100% usage for hours. In order to find what package installed this tracker as its dependencies, I utilized pactree.

Apparently, tracker3, tracker3-miners or anything closely related to this package helps index files and directories in Gnome environment, specifically file browser.

I noticed that there are two ways to find the dependents or the dependencies of a package in Arch Linux, offline or online method.

Offline Method (requires installation)

In order to install pactree, we cannot directly install it unless we compile and build the package manually however, it is available through package named pacman-contrib.

sudo pacman -S pacman-contrib

Once installed, we can check out the manual or quick instructions using -h flag or simply man pactree. One flag that I found to be very useful for my purpose was -r, it prints out reverse dependents of a package, exactly what we need. By default, it prints out all the dependencies for a specified package.

To find the reverse package dependents of tracker3-miners, we can simply run..

pactree -r tracker3-miners

The output of the previous command is as follows. From this output, we know that the package that utilizes high CPU usage was installed by nautilus and hence, nautilus is a problem.

tracker3-miners
└─nautilus

Alternative Offline Method

Simply trying to remove the package that you believe is problematic yields interesting response from pacman.

sudo pacman -Rs tracker3-miners

Output

checking dependencies...
error: failed to prepare transaction (could not satisfy dependencies)
:: removing tracker3-miners breaks dependency 'tracker3-miners' required by nautilus

Online Method (requires surfing the internet)

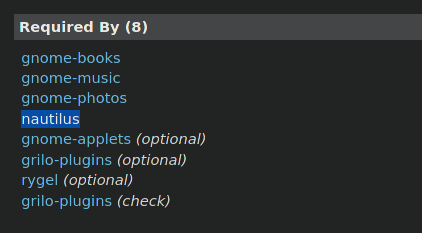
The other method, an online method is to search the package in Arch Linux’s package database. If we scroll down a little, we can notice two neatly organized columns with titles - Dependencies and Required By.

In the Required By column, we can notice the package nautilus, the package I had installed, hence, I found the culprit.

Simply removing the package with sudo pacman -Rs nautilus fixed the problem.